Okay, so I was messing around with some math stuff the other day and got stuck on something that I thought should be simple: figuring out the range of arccos. You know, that function that’s like the opposite of cosine? Yeah, that one.
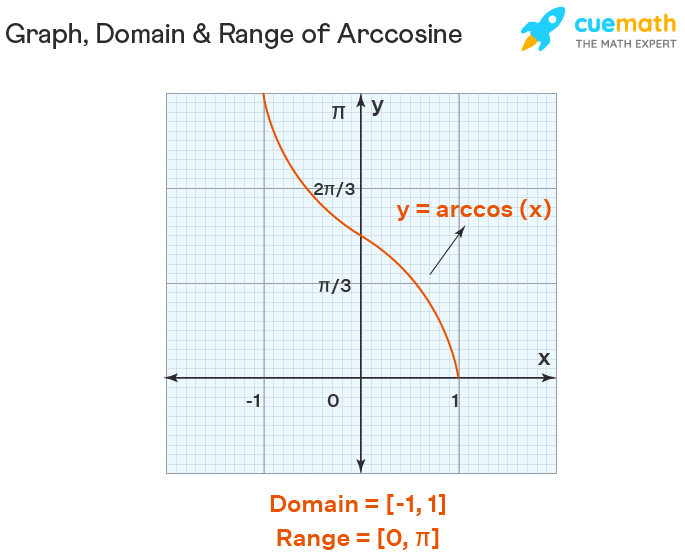
So I started by drawing out the cosine graph, that wavy line that goes up and down between -1 and 1. I remembered that the arccos is basically asking, “If I give you a value between -1 and 1, what angle would give me that value as its cosine?”
I grabbed my calculator and started plugging in some numbers. Like, what’s the arccos of 0.5? The calculator said 60 degrees, which is π/3 in radians. Okay, cool. But then I thought, wait a minute, cosine is a periodic function. It repeats itself, right? So there are actually tons of angles that could give you a cosine of 0.5.
That’s where I got a little confused. How do we decide which angle to pick for arccos? I mean, there’s a whole bunch of them! I did a little digging online and found out that mathematicians decided to restrict the range of arccos. They basically said, “Let’s just focus on the angles between 0 and π (or 0 to 180 degrees).” That way, arccos only gives you one answer, and it’s always within that range.
Here’s how I see it:
- Cosine goes from angles to values between -1 and 1.
- Arccos goes from values between -1 and 1 back to angles, but only between 0 and π.
So, to make sure arccos doesn’t get all confused with too many possible answers, we just take that chunk of the cosine wave that goes from 0 to π. It covers all the possible cosine values exactly once, and it keeps everything nice and tidy.

Why 0 to π, though?
Well, I learned that this is called the “principal branch” of arccos. I guess it’s like the main branch of a tree, and all the other possible angles are like smaller branches that we’re ignoring for now. It makes sense when you think about it. We need a standard way to define arccos so that everyone’s talking about the same thing.
So, yeah, that’s what I figured out about the range of arccos. It’s always between 0 and π, and that’s because we need a clear, single answer, and that’s the range that covers all the possible cosine values just once. Pretty neat, huh?